I’ve solved the recursive function problem.
Problem
Find the rule from the following example output, write the code for working it.
Input
Number N will be given representing the number of lines.
N is always \(3×2^k\). (3, 6, 12, 24, (k <=10)
Output
Print ‘*’ character the first to last line.
Example Input
24
Example Output
*
* *
*****
* *
* * * *
***** *****
* *
* * * *
***** *****
* * * *
* * * * * * * *
***** ***** ***** *****
* *
* * * *
***** *****
* * * *
* * * * * * * *
***** ***** ***** *****
* * * *
* * * * * * * *
***** ***** ***** *****
* * * * * * * *
* * * * * * * * * * * * * * * *
***** ***** ***** ***** ***** ***** ***** *****
From here
It looks quite different usually called print ‘*’ problems, isn’t it?
I just thought It is definitely the recursive function problem.
But the problem is finding the rule for using recursively and the output system.
Before I tried to solve this problem, I made the triangle output system.
From C++ standard, We didn’t have any terminal or console cursor move function.
I could figure out using the array but it’ll make a lot of empty space.
So I come up with using ‘map’.
Key is the number of lines and the value is the list of ‘*’ position.
Simply, the key is Y position value is the list of X position.
So I implemented add-point function at the X, Y coordinate and print triangle at the X, Y position using the add-point function.
Triangle’s drawing position is the left-top.
Like this:

So the code about above is:
map<int, vector<int>*> printlist;
int emptyCount = 0;
void addPrint(int x, int y)
{
if(printlist.find(y) == printlist.end())
{
printlist[y] = new vector<int>();
}
if(find(printlist[y]->begin(), printlist[y]->end(), x) == printlist[y]->end())
printlist[y]->push_back(x);
}
void printAll()
{
for(int i=0;i<printlist.size(); i++)
{
vector<int>* vec = printlist[i];
if(vec==nullptr)
{
cout<<endl;
continue;
}
sort(vec->begin(),vec->end());
int dif=vec->at(0);
int before = -1;
for(int j=0;j<vec->size();j++)
{
dif = vec->at(j) - before-1;
for(int k=0;k<dif;k++)
{
cout<<" ";
}
cout<<"*";
before = vec->at(j);
}
for(int p=before;p<emptyCount-2;p++)
cout<<" ";
cout<<endl;
}
}
void printTriangle(int x, int y)
{
addPrint(x+2,y+0);
addPrint(x+1,y+1);
addPrint(x+3,y+1);
addPrint(x+0,y+2);
addPrint(x+1,y+2);
addPrint(x+2,y+2);
addPrint(x+3,y+2);
addPrint(x+4,y+2);
}
‘emptyCount’ variable is used for print empty space after the final output and its value is N * 2 - 2.
‘dif’ variable is used for print empty space between previously printed ‘*’ and currently print position.
And the function printTriangle(0,0) is implemented experientially.
So When I call the function printTriangle(0,0) then it’ll be print like this:
*
* *
*****
So Let’s come back to the problem.
It is a recursive problem.
The drawing position of the triangle is left-top. And we can find the rule when N is 6.
The top triangle’s coordinate is (3, 0). It is figured out (0+N/2, 0).
And Left-Bottom triangle’s coordinate is (0,3). And it’s came up with (0, N/2).
the Right-Bottom triangle’s coordinate is (6,3). and it’s figured out (0+N, N/2).
This rule can be used when N is bigger.
That means we can write ‘the recursive function.
I drew above rules:
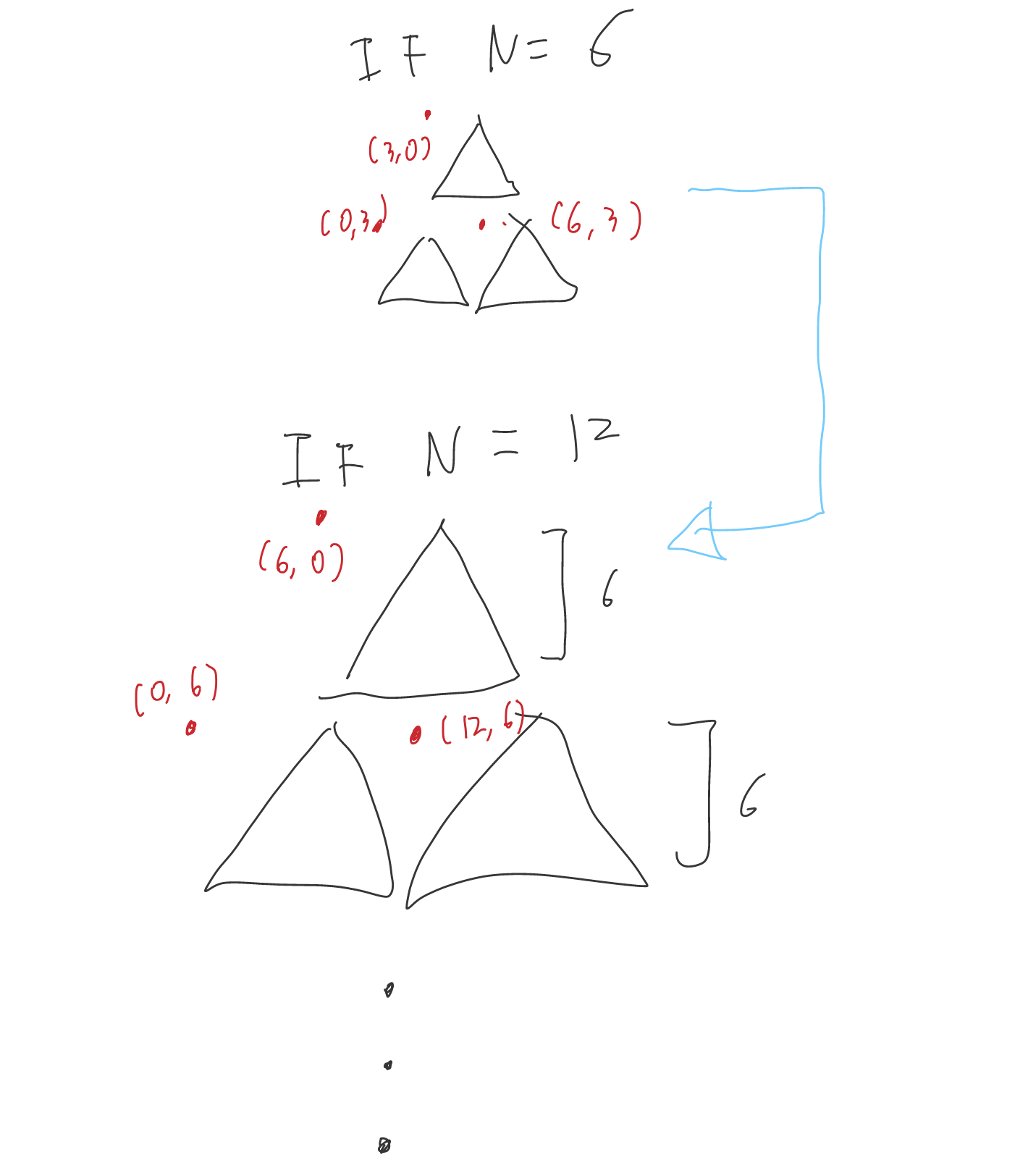
Let’s write the recursive function!
void recursive(int x,int y,int p)
{
if(p==6)
{
printTriangle(0+x,3+y);
printTriangle(6+x,3+y);
printTriangle(3+x,0+y);
}
else
{
recursive(x+p/2,y, p/2);
recursive(x,y+p/2, p/2);
recursive(x+p,y+p/2, p/2);
}
}
and… it’s solved!!!
Following codes is full source code for this problem!
#include <iostream>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;
map<int, vector<int>*> printlist;
int emptyCount = 0;
void addPrint(int x, int y)
{
if(printlist.find(y) == printlist.end())
{
printlist[y] = new vector<int>();
}
if(find(printlist[y]->begin(), printlist[y]->end(), x) == printlist[y]->end())
printlist[y]->push_back(x);
}
void printAll()
{
for(int i=0;i<printlist.size(); i++)
{
vector<int>* vec = printlist[i];
if(vec==nullptr)
{
cout<<endl;
continue;
}
sort(vec->begin(),vec->end());
int dif=vec->at(0);
int before = -1;
for(int j=0;j<vec->size();j++)
{
dif = vec->at(j) - before-1;
for(int k=0;k<dif;k++)
{
cout<<" ";
}
cout<<"*";
before = vec->at(j);
}
for(int p=before;p<emptyCount-2;p++)
cout<<" ";
cout<<endl;
}
}
void printTriangle(int x, int y)
{
addPrint(x+2,y+0);
addPrint(x+1,y+1);
addPrint(x+3,y+1);
addPrint(x+0,y+2);
addPrint(x+1,y+2);
addPrint(x+2,y+2);
addPrint(x+3,y+2);
addPrint(x+4,y+2);
}
void recursive(int x,int y,int p)
{
if(p==6)
{
printTriangle(0+x,3+y);
printTriangle(6+x,3+y);
printTriangle(3+x,0+y);
}
else
{
recursive(x+p/2,y, p/2);
recursive(x,y+p/2, p/2);
recursive(x+p,y+p/2, p/2);
}
}
void freeAll()
{
for(map<int,vector<int>*>::iterator i = printlist.begin();i!=printlist.end(); i++)
{
delete i->second;
}
}
int main()
{
int input=0;
cin>>input;
emptyCount = input*2;
if(input==3)
printTriangle(0,0);
else
recursive(0,0,input);
printAll();
freeAll();
return 0;
}
I think I’m very enjoying this problem!
